Multidimensional Scaling (MDS)

Multidimensional Scaling (MDS) is a technique for visualizing and analyzing high-dimensional data by mapping it to a lower-dimensional space, making it easier to observe and analyze. This feature is located in SPSSAU -> Comprehensive Evaluation -> Multidimensional Scaling (MDS).

SPSSAU Operations

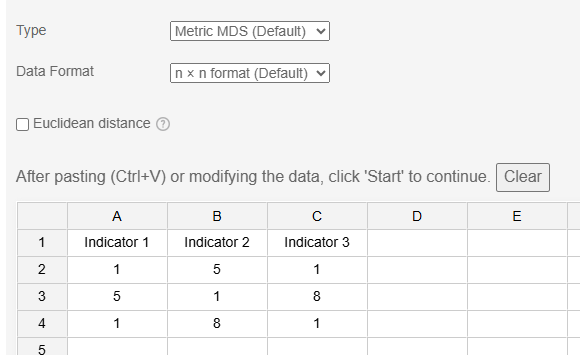
To perform the analysis, paste (or edit) the data into the data frame and click 'Start'. SPSSAU involves three key parameters: MDS Type, Data Format, and Calculate Euclidean Distance.

MDS Type: SPSSAU provides two methods: 'Metric MDS' (default) and 'Non-metric MDS'.

Data Format: SPSSAU supports two data formats: n×n Format and Original Data Format.

Calculate Euclidean Distance: If the data format is 'n×n Format', selecting this parameter will first compute the Euclidean distance. If not selected, Euclidean distance is not calculated. If the data format is ' Original Data Format', SPSSAU will always compute the 'Euclidean distance' regardless of this setting.

SPSSAU Data Format

If using the n×n Format, the data appears as shown in the figure above. The main diagonal contains values of 1, representing the distance of each item to itself. The remaining values represent the distances between different research objects.

If using the Original Data Format, the data appears as shown above, where the first column lists the names of the research objects, and the numbers represent their values on specific indicators.

Algorithm

SPSSAU utilizes the Scikit-learn package to implement the MDS algorithm. For more details, please refer to the official documentation: https://scikit-learn.org/stable/modules/manifold.html#multi-dimensional-scaling-mds

The corresponding Python parameter settings are as follows:

• n_components = 2
• metric = True / False (True for Metric MDS and False for Non-metric MDS)
• max_iter = 300
• eps = 1e-9,
• random_state = 10000
• dissimilarity = "precomputed"
• n_init = 1