Data Envelopment Analysis (DEA)

Data Envelopment Analysis (DEA) is a non-parametric method used to assess the relative efficiency of decision-making units (DMUs). It is located in SPSSAU -> Comprehensive Evaluation -> DEA.

SPSSAU Operations

To perform the analysis, drag the analysis items to the right box and click 'Start.' SPSSAU involves three parameters: Type, Non-negative Shift, and Save Efficiency.

Type: Default is BCC (VRS, Variable Returns to Scale), with an optional CCR type (CRS, Constant Returns to Scale).

Non-negative Shift: When selected, if any column contains values ≤ 0, the system shifts all values by adding the absolute value of the minimum plus 0.01 to ensure positive values for normal computation.

Save Efficiency: When selected, SPSSAU saves Technical Efficiency (TE), Scale Efficiency (SE), and Overall Efficiency (OE) under the respective titles: TE_****, SE_****, and OE_****.

SPSSAU Data Format

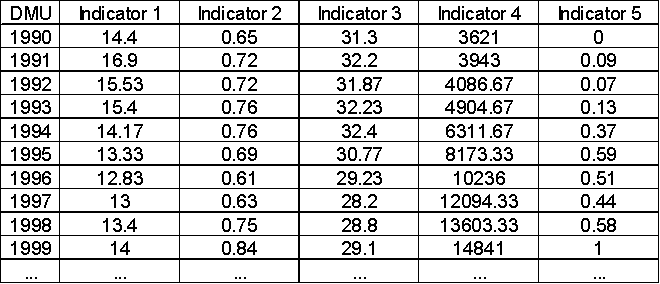
In DEA analysis, a single column represents the DMU. If no such column is specified or if it is not placed under 'Label' in the analysis, SPSSAU will default to naming them sequentially as Item 1, Item 2, etc. Each indicator occupies one column, whether it is an input or output indicator.

Algorithm

1.Identify DMUs

Select the DMUs (e.g., companies, departments) to be evaluated and define their input and output indicators. Suppose there are DMUs, each with m input variables and q output variables. The data can be represented using the following matrix:

$$X=\left(\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1m}\\ x_{21}& x_{22}& \cdots & x_{2m}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{nm}\end{array}\right)$$ $$Y=\left(\begin{array}{cccc}{y}_{11}& y_{12}& \cdots & y_{1q}\\ y_{21}& y_{22}& \cdots & y_{2q}\\ ⋮& ⋮& \ddots & ⋮\\ y_{n1}& y_{n2}& \cdots & y_{nq}\end{array}\right)$$

2.Non-negative Shift

$$x_{ij}=|min(x_{\ast j})|+0.01$$

If this parameter is selected and the precondition x_*j <= 0 is met, the system will perform the above shift.

3.Efficiency Value Definition

SPSSAU defines 'efficiency value' as output / input. If the input is relatively low while the output is relatively high, the 'efficiency value' will be higher; conversely, if the input is relatively high while the output is relatively low, the 'efficiency value' will be lower. The formula is as follows:

$$h=\frac{\sum _{r=1}^q{u}_r{y}_r}{\sum _{i=1}^m{v}_i{x}_i}$$

The number of input variables X is m, and the number of output variables Y is q. v represents the coefficient for each input variable X, and u represents the coefficient for each output variable Y. Both u and v are values to be solved. The constraints are as follows:

$$maxh=\frac{\sum _{r=1}^q{u}_r{y}_r}{\sum _{i=1}^m{v}_i{x}_i}$$ $$h\le 1,u\ge 0,v\ge 0$$

4.Construct the DEA Model

SPSSAU provides two models: CCR and BCC. Their respective Charnes-Cooper transformations are as follows:

CCR Model (CRS, Constant Returns to Scale):

$$min\theta$$ $$s.t.\{\begin{array}{c}\sum _{j=1}^n{\lambda }_j{X}_j+S^{-}=\theta X_{j0}\\ \sum _{j=1}^n{\lambda }_j{X}_j-S^{+}=Y_{j0}\\ S^{+},S^{-},{\lambda }_j\ge 0\\ \mathrm{j}=1,2,\cdots n\end{array}$$

BCC Model (VRS, Variable Returns to Scale):

$$min\theta$$ $$s.t.\{\begin{array}{c}\sum _{j=1}^n{\lambda }_j{X}_j+S^{-}=\theta X_{j0}\\ \sum _{j=1}^n{\lambda }_j{X}_j-S^{+}=Y_{j0}\\ S^{-},S^{+},{\lambda }_j\ge 0\\ \mathrm{j}=1,2,\cdots n\\ \sum _{j=1}^n{\lambda }_j=1\end{array}$$

θ represents the efficiency value, λ=(λ1,λ2,…,λn)^T is the weight vector, X_j represents the input of DMU j, and Y_j represents the output of DMU j. S^- and S⁺ are the input and output slack variables of DMU j, respectively. The constraints ensure S^-, S⁺, and λ are all non-negative.

5.Solve the DEA Model

SPSSAU utilizes the pulp package for mathematical computation, obtaining TE (Technical Efficiency), SE (Scale Efficiency), and OE (Overall Efficiency), along with indicators S^- and S⁺, and outputs the results. The relationship among these metrics is defined as OE = TE × SE.

OE=1 indicates DEA efficiency, while OE < 1 indicates DEA inefficiency.

TE=1 signifies technical efficiency, whereas TE < 1 suggests room for technical improvement.

SE=1 indicates constant returns to scale (optimal state), SE < 1 implies increasing returns to scale (indicating the possibility of expanding for higher efficiency), and SE > 1 suggests decreasing returns to scale (indicating that downsizing may improve efficiency).

S- indicates 'how much input reduction is needed to achieve target efficiency.'

S+ indicates 'how much output increase is needed to achieve target efficiency.'

By examining the three indicators (OE, S-, and S+), DEA validity can be determined: If OE = 1 and both S- and S+ are 0, DEA is 'strongly efficient'. If OE = 1 but either S- or S+ is greater than 0, DEA is 'weakly efficient'. If OE < 1, DEA is 'inefficient'.