Best Worst Method (BWM)

Best Worst Method (BWM) is an effective multi-criteria decision-making approach primarily used to determine the weight of various factors. It is located in SPSSAU ->Comprehensive Evaluation -> Best Worst Weight (BWM).

SPSSAU Operations

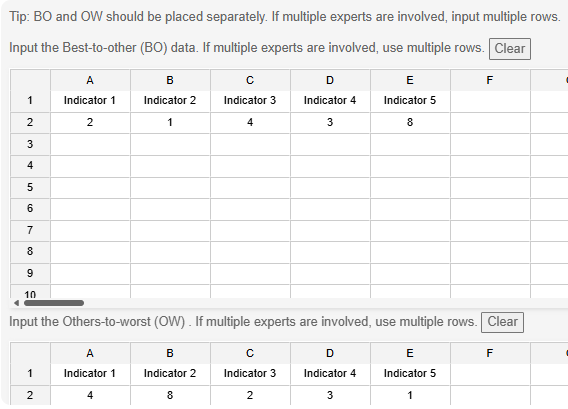
To conduct the analysis, input Best-to-other (BO) data and Others-to-worst (OW) data into their respective data frames and click 'Start'. Note: If multiple experts provide ratings, there will be multiple rows of BO or OW data.

SPSSAU Data Format

Details regarding Best-to-other (BO) data and Others-to-worst (OW) data are as follows.

Algorithm

1.Define Criteria Indicators

First, all indicators relevant to the decision-making problem must be identified. The number of indicators is typically limited. Experts rate these indicators and determine the best (optimal) indicator and worst (least optimal) indicator. Scores are assigned based on these two indicators. A predefined scale (e.g., a 1~9 scale, where 1 represents the least important and 9 represents the most important) is used for rating.

Best-to-other (BO) data represents the relative importance of the best indicator compared to each indicator. Others-to-worst (OW) data represents the relative importance of each indicator compared to the worst indicator. For instance, if there are five indicators, each expert will provide 5 BO values and 5 OW values, totaling 10 values. If multiple experts are involved, the process is repeated accordingly. In BO data, a higher value indicates that the indicator is less important. In OW data, a higher value indicates that the indicator is more important.

2.Construct the Comparison Matrix

A ratio matrix is constructed based on the best and worst combination indicators obtained in the previous step.

BO = (a_B1 a_B2 a_B3 ... a_Bn) OW = (a_1W a_2W a_3W ... a_nW)

• In the equation:
• n represents the number of experts.
• a_Bj represents the relative score of the best indicator compared to indicator j.
• a_jW represents the relative score of indicator j compared to the worst indicator.

3.Calculate Weights

The criterion weights are determined using the following optimization model:

$$minϵ$$ s.t. $$|\frac{W_B}{W_j}-a_{Bj}|\le ϵ$$ $$|\frac{w_j}{w_W}-a_{jW}|\le ϵ$$

Constraints:

$$\sum _{j=1}^n{w}_j=1$$ $$w_j\ge 0,{\mathrm{\forall }}_j$$

• ϵ is the error term; the smaller the value, the better.
• w_B represents the weight of the best criterion.
• w_W represents the weight of the worst criterion.
• w_j represents the weight of criterion j.
• a_Bj represents the comparison value of the best criterion relative to criterion j.
• a_jW represents the comparison value of criterion j relative to the worst criterion.

4.Consistency Test

To ensure consistency in judgment, the following formula is used for verification:

$$CR=\frac{ϵ}{CI}$$

CI is determined based on the number of indicators, as shown below:

Consistency Index(CI)
Order	1	2	3	4	5	6	7	8	9
CI	0.00	0.44	1.00	1.63	2.30	3.00	3.73	4.47	5.23

CR is the consistency ratio. Generally, the smaller the value, the higher the consistency. If CR > 0.5, reassessment of judgments may be necessary.