Analytic Hierarchy Process (AHP)

Analytic Hierarchy Process (AHP) is commonly used to calculate weights based on expert evaluations. SPSSAU provides two calculation methods: Sum Product Method and Square Root Method, with the former set as the default. This function is located in SPSSAU -> Comprehensive Evaluation -> Analytic Hierarchy Process (AHP).

SPSSAU Operations

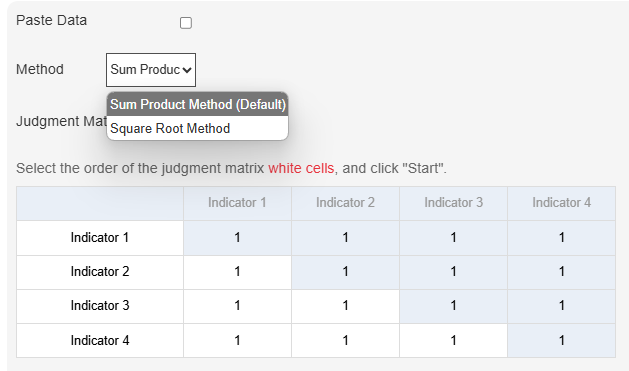
SPSSAU offers two ways to enter data: enter data directly and paste data (judgment matrix). The figure above illustrates the data entry process. Researchers can edit indicator names and the values in the white cells. Since the judgment matrix is a 'lower triangular' symmetric matrix, any changes in the 'white'-background cells will automatically update the corresponding 'blue'-background cells.

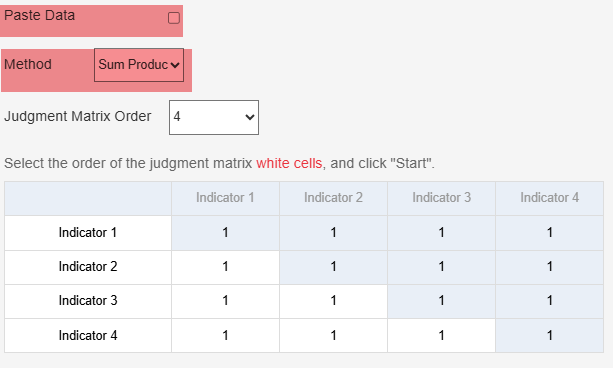
The figure above demonstrates the paste data process.

SPSSAU Data Format

As shown in the figure above, the data format of AHP (judgment matrix) is unique. Researchers can edit indicator names and values in the white cells. Since the judgment matrix is a 'lower triangular' symmetric matrix, any changes in the 'white'-background cells will automatically update the corresponding 'blue'-background cells. Alternatively, researchers can paste the judgment matrix directly for analysis.

Sum Product Method

The calculation steps and formulas are as follows:

1.Construct the Judgment Matrix

Experts compare each evaluation metric in pairs, forming an n * n judgment matrix A:

$$A=\left[\begin{array}{cccc}\mathit{1}& a_{\mathit{12}}& \dots & a_{\mathit{1}\mathit{n}}\\ \frac{\mathit{1}}{a_{\mathit{12}}}& \mathit{1}& \dots & a_{\mathit{2}\mathit{n}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\mathit{1}}{a_{\mathit{1}\mathit{n}}}& \frac{\mathit{1}}{a_{\mathit{2}\mathit{n}}}& \dots & \mathit{1}\end{array}\right]$$

a_ij represents the importance rating of i relative to j.

2.Calculate the Weight Vector

(1)Normalize each column:

$$a_{i{j}^{\prime }}=\frac{a_{ij}}{\sum _{i=\mathit{1}}^n{a}_{ij}}$$

(2)Calculate the average of each row as the weight:

$$w_i=\frac{\mathit{1}}{n}\sum _{j=\mathit{1}}^n{a}_{i{j}^{\prime }}$$

3.Consistency Test

(1)Calculate the Consistency Index (CI)

$${\lambda }_{max}=\frac{\sum (Aw{)}_i}{n{w}_i}$$

A is the judgment matrix. w is the weight vector. n is the matrix order.

$$CI=\frac{{\lambda }_{max}-n}{n-\mathit{1}}$$

λ_max is the maximum eigenvalue of the judgment matrix.

(2)Calculate the Consistency Ratio (CR)

Calculate RI, as shown in the table below.

RI Table
n Order	3	4	5	6	7	8	9
RI	0.52	0.89	1.12	1.26	1.36	1.41	1.46
n Order	10	11	12	13	14	15	16
RI	1.49	1.52	1.54	1.56	1.58	1.59	1.5943
n Order	17	18	19	20	21	22	23
RI	1.6064	1.6133	1.6207	1.6292	1.6358	1.6403	1.6462
n Order	24	25	26	27	28	29	30
RI	1.6497	1.6556	1.6587	1.6631	1.667	1.6693	1.6724
n Order	31	32	33	34	35	36	37
RI	1.6755	1.6773	1.68	1.6828	1.6837	1.6864	1.6883
n Order	38	39	40	41	42	43	44
RI	1.6903	1.6921	1.6929	1.6947	1.6958	1.6985	1.6991
n Order	45	46	47	48	49	50	51
RI	1.7006	1.7015	1.7023	1.7045	1.7056	1.7065	1.7066
n Order	52	53	54	55	56	57	58
RI	1.7071	1.709	1.71	1.7109	1.7113	1.7123	1.7127

Calculate CR: CR = \frac{CI}{RI}

When CR < 0.1, the consistency is considered acceptable.

Square Root Method

1.Judgment Matrix

Experts compare each evaluation metric in pairs, forming an n * n judgment matrix A:

$$A=\left[\begin{array}{ccccc}1& a_{12}& a_{13}& \dots & a_{1n}\\ \frac{1}{a_{12}}& 1& a_{23}& \dots & a_{2n}\\ \frac{1}{a_{13}}& \frac{1}{a_{23}}& 1& \dots & a_{3n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \frac{1}{a_{1n}}& \frac{1}{a_{2n}}& \frac{1}{a_{3n}}& \dots & 1\end{array}\right]$$

a_ij represents the importance rating of i relative to j.

2.Weight Vector

The weight vector W is obtained by computing the eigenvalues and eigenvectors of the judgment matrix. The eigenvector can be derived using the following formula:

AW = λ_maxW

λ_max is the maximum eigenvalue of matrix A.

3.Consistency Test

Calculate CI: CI = \frac{{\lambda }_{max}-n}{n-1}

Calculate RI, as shown in the table below.

RI Table
n Order	3	4	5	6	7	8	9
RI	0.52	0.89	1.12	1.26	1.36	1.41	1.46
n Order	10	11	12	13	14	15	16
RI	1.49	1.52	1.54	1.56	1.58	1.59	1.5943
n Order	17	18	19	20	21	22	23
RI	1.6064	1.6133	1.6207	1.6292	1.6358	1.6403	1.6462
n Order	24	25	26	27	28	29	30
RI	1.6497	1.6556	1.6587	1.6631	1.667	1.6693	1.6724
n Order	31	32	33	34	35	36	37
RI	1.6755	1.6773	1.68	1.6828	1.6837	1.6864	1.6883
n Order	38	39	40	41	42	43	44
RI	1.6903	1.6921	1.6929	1.6947	1.6958	1.6985	1.6991
n Order	45	46	47	48	49	50	51
RI	1.7006	1.7015	1.7023	1.7045	1.7056	1.7065	1.7066
n Order	52	53	54	55	56	57	58
RI	1.7071	1.709	1.71	1.7109	1.7113	1.7123	1.7127

Calculate CR: CR = \frac{CI}{RI}

When CR < 0.1, the consistency is considered acceptable.